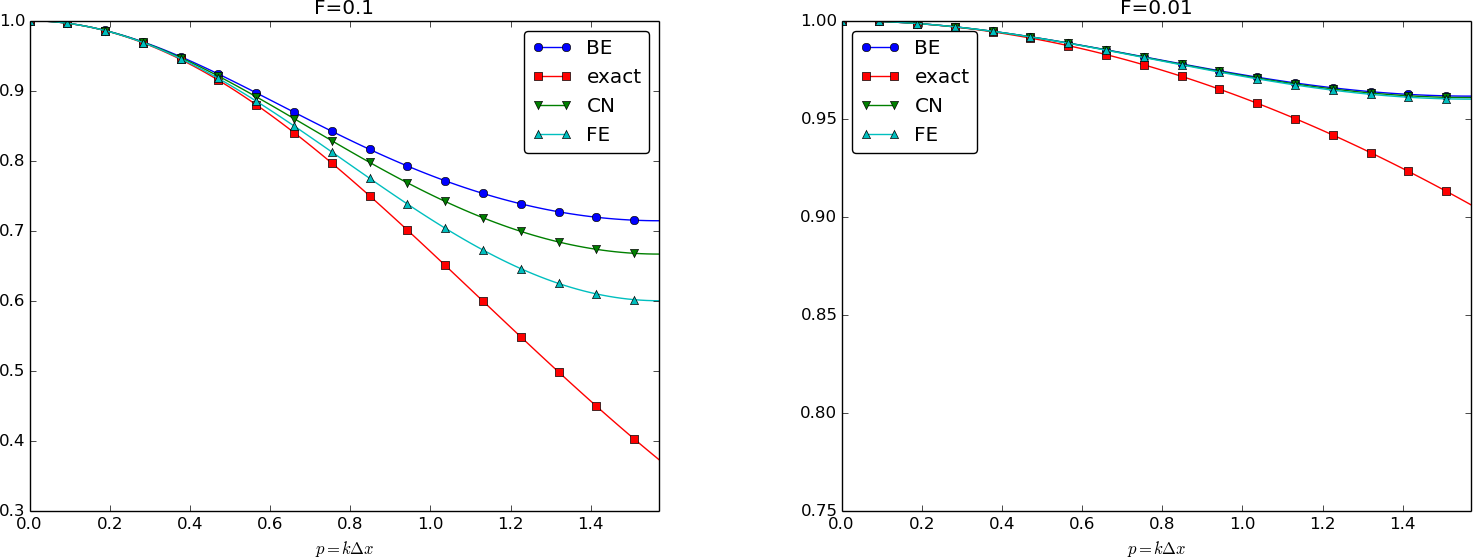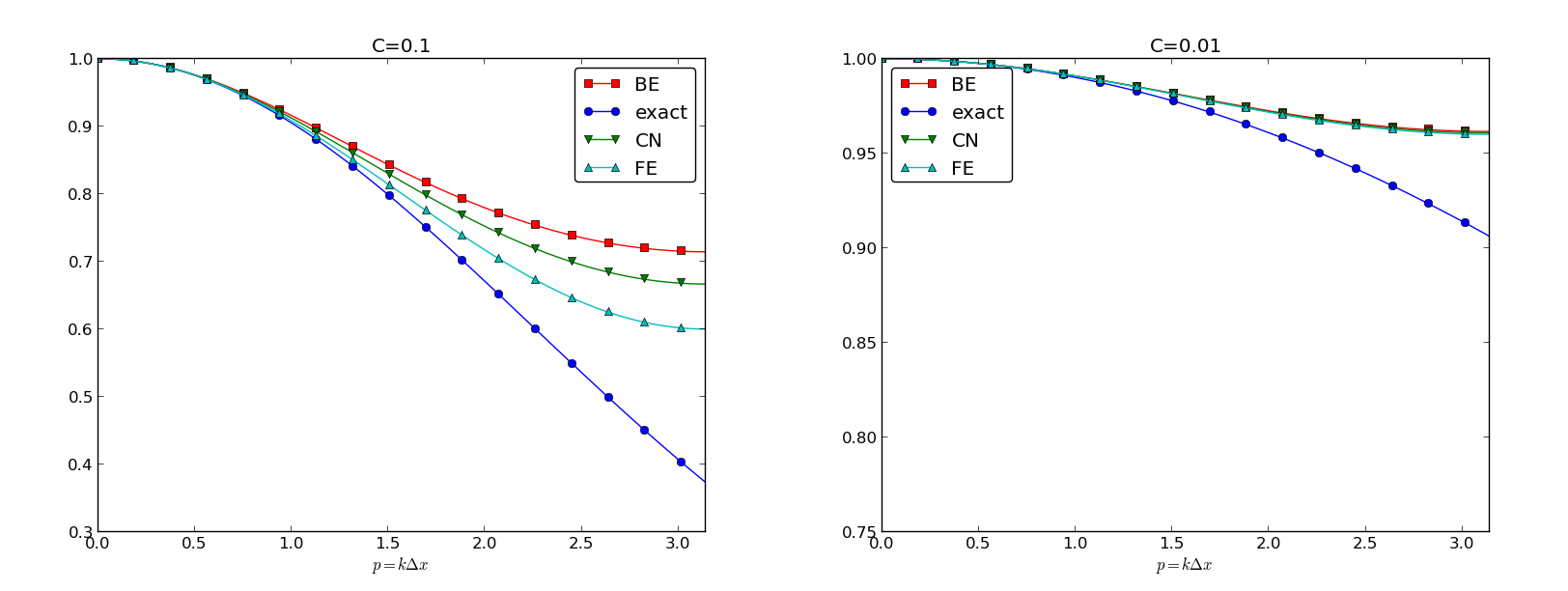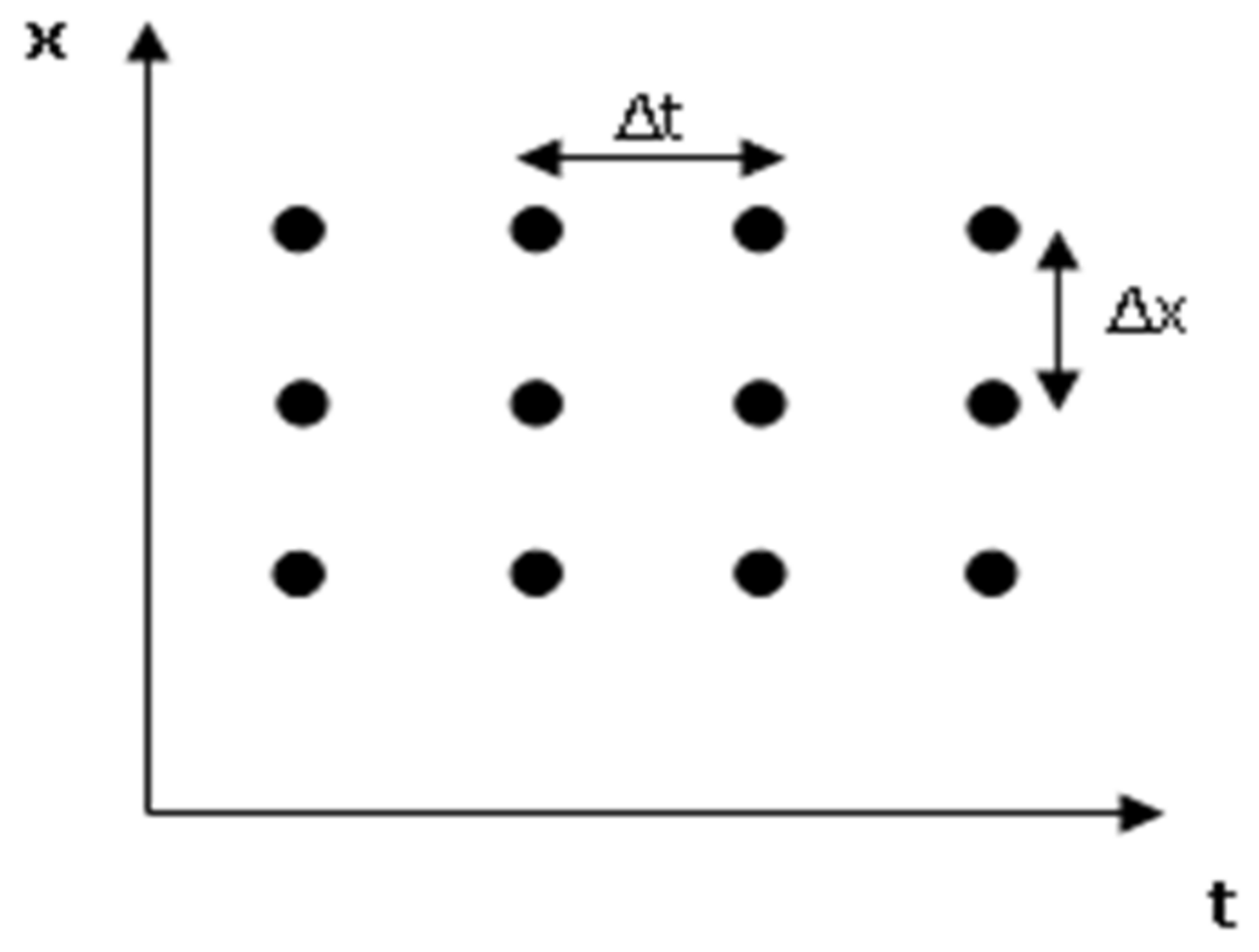
Applied Sciences | Free Full-Text | Convergency and Stability of Explicit and Implicit Schemes in the Simulation of the Heat Equation | HTML
Python Finite Difference Schemes for 1D Heat Equation: How to express for loop using numpy expression - Computational Science Stack Exchange
Finite difference methods for diffusion processes
PDF) FDM for Heat Equation
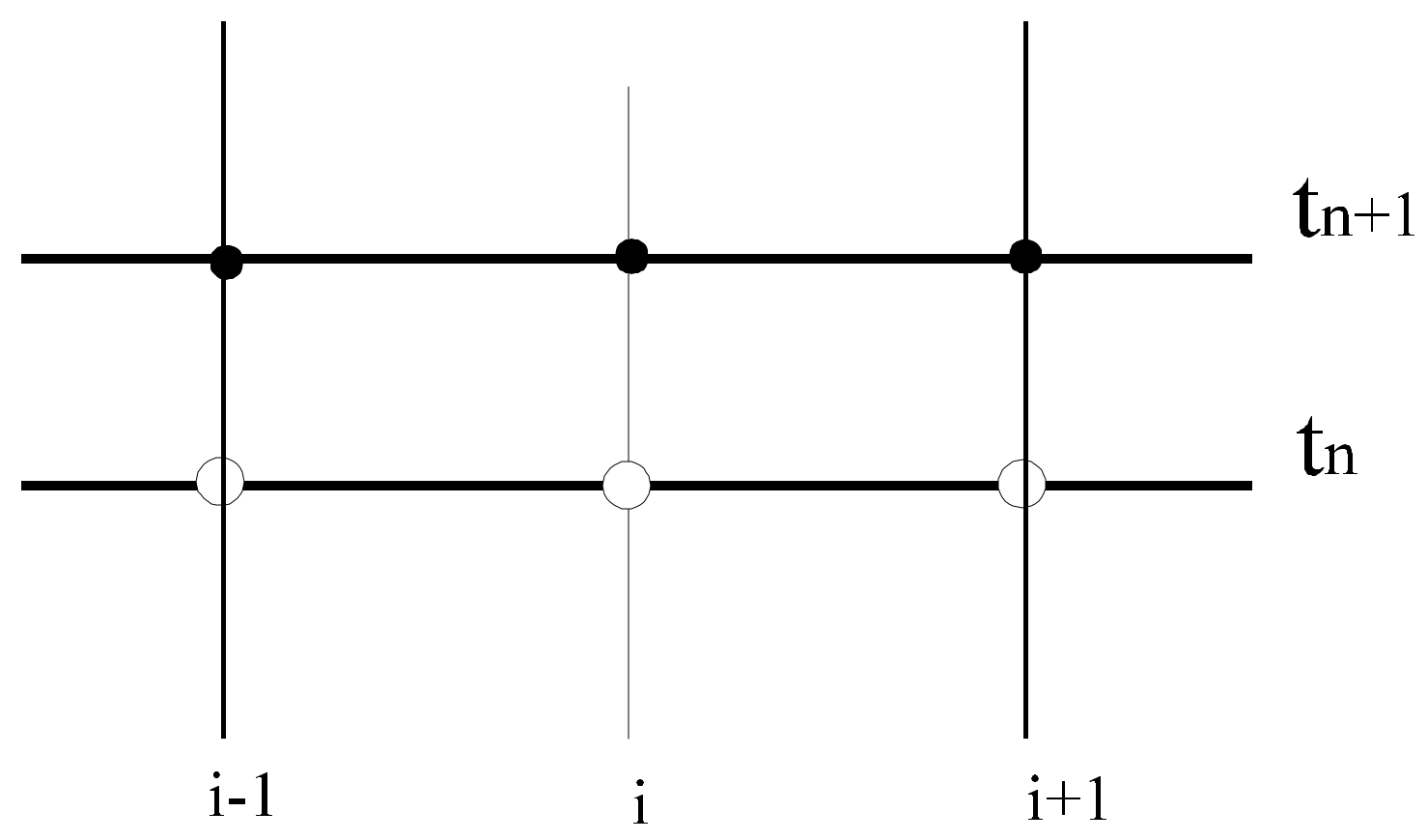
Applied Sciences | Free Full-Text | Convergency and Stability of Explicit and Implicit Schemes in the Simulation of the Heat Equation | HTML
Applied Sciences | Free Full-Text | Convergency and Stability of Explicit and Implicit Schemes in the Simulation of the Heat Equation | HTML
Solving 2D Heat Equation Numerically using Python | Level Up Coding
Problem 1 (Submit) Consider the 1D heat equation ut = | Chegg.com
The 1D diffusion equation
BEM/FVM conjugate heat transfer analysis of a three‐dimensional film cooled turbine blade | Emerald Insight
A comparison between the approximate numerical solution using FDM and... | Download Scientific Diagram
Quantized classical response from spectral winding topology | Nature Communications
Solved The 2D diffusion equation u_t = D nabla^2 u is | Chegg.com
Applied Sciences | Free Full-Text | Convergency and Stability of Explicit and Implicit Schemes in the Simulation of the Heat Equation | HTML
A comparison between the approximate numerical solution using FDM and... | Download Scientific Diagram
A comparison between the approximate numerical solution using FDM and... | Download Scientific Diagram
Cu2Se-based thermoelectric cellular architectures for efficient and durable power generation | Nature Communications
PDF) Finite difference methods for fractional differential equations
180 questions with answers in MATHEMATICA | Science topic
FTCS solution to the heat equation at t = 1 obtained with r = 2. The... | Download Scientific Diagram
Applied Sciences | Free Full-Text | Convergency and Stability of Explicit and Implicit Schemes in the Simulation of the Heat Equation | HTML
Computer-Aided Engineering (CAE) | SpringerLink
Fast numerical approximation for the space-fractional semilinear parabolic equations on surfaces | Request PDF
NESTLE
